Science Clock Series: Part XI

Today's number comes from astronomy and is given by:

\[\approx\ \text{diameter of ♃(in \(\beta\); \(\oplus=1\beta\)}\] This is a slightly roundabout way of saying "approximately the diameter of Jupiter in Earth-diameters." Let's look at it a little more closely:

First of all, what in the world is ♃ supposed to be? Or \(\oplus\)? To answer those questions we need to go back in time. About 2,000 years in fact, give or take. You see, one thing that I've learned from idly inspecting ancient writing, whether written, inscribed, or etched, is that ancient people liked to abbreviate.

Although it surprised me at first, this is entirely reasonable when you think about it; we do it all the time in everyday life, especially with the proliferation of instant messaging. Ancient peoples had to write everything by hand, which in my opinion is very dull and tiresome. You start looking for ways to reduce the amount you have to write, and before you know it you've got abbreviations all over the place.

Anyway, writing goes back a long time, but for much of history it was limited to a thin slice of the most educated in society. The study of astronomy also goes back a long time, and was one of the most common subjects for that educated elite to study, given its importance to pre-Industrial societies in helping to determine things like the proper time to plant and harvest crops in order to ensure everyone didn't starve over the winter.

Put those fact together, and people have been writing about astronomy for a very long time. Some of the oldest writings we find have been discovered to be about astronomy. Since it was so important, and given that most people like to save time and effort when writing, ancient astronomers in the Hellenistic period around the time of Christ came up with a set of symbols to refer to the "planets."

Note that the word "planets" in this context refers to the seven "planets" of the Ptolemaic (and originally Aristotelian) heliocentric system: the Sun, the Moon, Mercury, Venus, Mars, Jupiter, and Saturn.These are the objects which, if you're familiar with the night sky, appear to move across it against the background of the fixed stars. Anyway, ancient astronomers came up with symbols for them that were used up through the Renaissance period. In fact, their use was so common that when astronomers such as William Herschel started discovering new planets astronomers rapidly came up with new symbols for them too. Anyway, here's a table with the symbols for the Sun, and the eight planets discovered before 1900:
\begin{align*}
\text{Sun}&\dots☉\\
\text{Mercury}&\dots☿\\
\text{Venus}&\dots♀\\
\text{Earth}&\dots\oplus\\
\text{Mars}&\dots♂\\
\text{Jupiter}&\dots♃\\
\text{Saturn}&\dots♄\\
\text{Uranus}&\dots♅\\
\text{Neptune}&\dots♆
\end{align*}You may be familiar with the symbols for Mars and Venus, as they have come to stand for “male” and “female” respectively in modern usage. Other than that, the only symbols commonly used in astronomy any more are the ones for the Sun and Earth. It's standard practice in astronomical journals for the symbols \(\text{R}_☉\), \(\text{M}_☉\), and \(\text{L}_☉\) to stand for the mass, radius, and luminosity of the Sun, respectively (and similarly for the Earth using the symbol for Earth).

It might give you some indication just how little known these symbols are today if I told you that right up until I looked them up to write this post I thought the symbol for Jupiter on my clock stood for Neptune!

Now that I know it stands for Jupiter, we can look at what the clock actually says: approximately the diameter of Jupiter in terms of “beta”, where “Earth” = 1 “beta.” I actually looked up beta to make sure there wasn't some special use for it that I wasn't aware of and couldn't find anything, so I'm not entirely sure what the point of introducing it only to immediately define it as one Earth was. Anyway, if we then check with the diameters of both Earth and Jupiter, we find that Jupiter does indeed have a diameter about 10.9377 times greater than Earth's.

So there you have it. And I realize this post isn't actually as short as I promised last time, though hopefully it was still interesting. There's a lot related to the astronomical symbols that I didn't cover, such as the fact that several were created for the first nineteen asteroids discovered before people realized that creating unique symbols for every asteroid would be effectively impossible and gave up (given that we now know of over a hundred thousand asteroids and suspect there may be ten times that number in the solar system, we can see that this was a good decision!).

Anyway, check back for the final post in this series, with a number from meteorology! Click here to jump directly to it.

Science Clock Series: Part X

It's been a while since my last post, and I figured you all deserve an explanation. I was in Nebraska all last week attending my grandfather's funeral, immediately after serving as a groomsman for a wedding in Kona. It's been a hectic fortnight. Between helping out around the family farm and catching up with relatives I haven't seen in years, this blog got put on the back burner. I'm now back in Hawaii, however, and getting back into the swing of things.

Anyway, today's number comes from both physics and biology, and is given by:

\[\lambda\ \text{of human body heat (in \(\mu\)m)}\] The Greek letter lambda \((\lambda)\) in this equation stands for “wavelength,” specifically the wavelength of the electromagnetic radiation given off by an object at average human body temperature. The symbol \(\mu\) is the Greek letter mu, and is an SI prefix denoting micro-, or one-millionth of something. So a micrometer is a millionth of a meter.

To understand this subject fully requires a short history lesson, and an understanding of the term “black body.” A black body is an idealized object that absorbs all electromagnetic energy that hits it, no matter what angle it hits at or how powerful it is. Being an ideal object, true black bodies don't exist in nature, but many things come pretty close. It's important to realize that a black body may not (and in reality will not) be actually black. A black body at any temperature above absolute zero (that is, all of them) will emit electromagnetic radiation in a characteristic energy distribution called “black-body radiation” that depends only on the temperature of the object: not what it's made of, not its shape, just its temperature. If the temperature is hot enough, a black body will emit light in the visible portion of the spectrum and visibly glow.

One example of a class of objects that approximate black bodies is stars. This may seem strange to you, because stars are anything but black – but it goes back to what I said earlier. When you think about it, stars really don't reflect any of the electromagnetic radiation that hits them. They absorb it, then re-emit it in a characteristic black-body spectrum. (It's not perfect because the presence of various elements in stars modifies it somewhat, but it's close enough to be able to measure the temperature of stars by measuring the amount of light they give off over all parts of the spectrum.)

Now, although there are no true black bodies in the universe, most things actually come pretty close. Some brilliant physicists in the late 19th and early 20th centuries formulated a couple of equations that describe the amount of electromagnetic radiation given off by a black body, per either unit wavelength or frequency. Once you know that, you can figure out where exactly on the spectrum an object is radiating most strongly at. A German physicist by the name of Wilhelm Wien deduced what is now known as Wien's Displacement Law in 1893. In symbols, it looks like: \[\lambda_{\text{max}}T=b\]In words, it says that as a black body (which is a good approximation for most objects remember) gets hotter, the wavelength at which it radiates most strongly becomes shorter and shorter; or alternatively, it produces more energetic light.  The Greek letter \(\lambda\) (lambda) stands for wavelength, the T stands for the absolute temperature in kelvins, and b is a quantity known as Wien's Displacement Constant, approximately equal to \(2.8977685\times10^{-3}\,\text{m}\cdot\text{K}\).

Now that we have an equation to use, it's a simple matter of algebra and plugging in numbers. Rearranging it to solve for the wavelength we get \(\lambda_{\text{max}}=b/T\). Despite what we all learned growing up, there isn't actually such a thing as a “normal” human body temperature; it varies by individual, time of day, state of the body itself, and many other factors. However, a value of 98.6 ºFarenheit works well enough as a good “average” temperature, so let's go ahead and use that. Converting to the Kelvin scale, we have:
\begin{align} [\text{K}]&=([^\circ\text{F}]+459.67)\times\frac{5}{9}\\
&=(98.6+459.67)\times\frac{5}{9}\\
&=310\ \text{kelvins}\end{align}Plugging that number in for the temperature in Wien's Displacement Law gets us:
\begin{align}
\lambda_{\text{max}}&=\frac{b}{T}\\
&=\frac{ 2.8977685\times10^{-3}\,\text{m}\cdot\text{K}}{310\,\text{K}}\\
&=9.34\times10^{-6}\,\text{meters}
\end{align}This is great and all, but our answer's in meters, not micrometers (\(\mu\)m) as it needs to be. One micrometer is \(1\times10^{-6}\) meters, however, so we need merely convert to get \(9.34\,\mu\)m. Which is fairly close to ten (within 10%), but actually closer still to nine. Oh, well. It was approximate.

This 9.34 \(\mu\)m, by the way, is a wavelength that corresponds to the far infrared. We humans constantly radiate at a range of wavelengths – near infrared on the shorter side, for example, sub-millimeter on the longer – but that wavelength (or near to is) tends to be where we radiate most strongly. And there's really not much we can do about it, since as endothermic creatures our bodies try to keep themselves in a tight specific temperature range. Though I can't think of any reason you'd want to change your peak radiating wavelength. We can't see in infrared, so it doesn't really matter. (If you're curious, it requires being a few hundred degrees hotter before the peak wavelength shifts into the visible portion of the spectrum and things start visibly glowing. If you have an electric stove, you can see this effect in action as it heats up: the point where it starts to glow is when it becomes hot enough to start radiating significantly in the visible region.)

Anyway, that was quite the lengthy post. Tune in next time for a much shorter one where we look at a number from astronomy again! Click here to jump directly to the next part.

Science Clock Series: Part IX

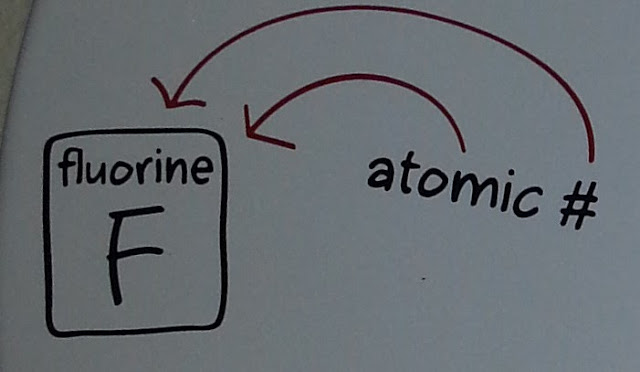
Today's number comes from chemistry, and is given by:

This one is quite straightforward; it's just the atomic number of the element fluorine.

As you probably remember from chemistry class, each element is uniquely described by something called its atomic number. This number is simply the number of protons in the nuclei of the atoms of that element. The number of protons determines how many electrons make an electrically balanced atom, and also how many electrons the atom will strive to attain (which are only the same number in the case of the noble gases, and hydrogen, somewhat).

You see, due to some slightly complicated features in quantum mechanics that I should talk about some day, not all electron configurations are created equal in energy. Many atoms, especially of the lighter elements, try to reach the same number of electrons as the noble gas closest in atomic number to them because that represents the lowest possible energy state for them.

Fluorine is a fairly light element. Its atomic number, nine, is just above oxygen (eight), and just below the noble gas neon (ten). It therefore wants to gain one more electron to bring it into a lower energy state. Now, if you know your chemistry, you know that oxygen is a highly, highly reactive element. Fires and explosions? Caused pretty much entirely by extremely rapid reaction of oxygen in the air with certain materials. From a biological standpoint, oxygen is pretty dangerous stuff if it gets where it isn't supposed to be because it can react with so much delicate biological machinery (which makes it even more amazing that our bodies run on the stuff). Single oxygen atoms that get loose in the body are classified as free-radicals, and can contribute to cell mutations and cancer if they react with DNA. Even in bulk, diatomic oxygen (the kind we breathe) can be dangerous if you get too much of it, in a condition known as oxygen toxicity.

Now, as bad as oxygen is, fluorine is worse. Much worse. It is the most reactive and electronegative element in the universe. Oxygen can actually exist in the Earth's atmosphere for a fairly long time as a diatomic molecule. Fluorine is much too unstable for that. Although it can (and does) form a diatomic molecule when isolated by itself, once free from containment it vigorously sets to work oxidizing  anything it comes into contact with  extremely rapidly. Quite a lot of substances will burn frighteningly quickly upon exposure to pure fluorine, including things we don't normally think of as flammable, such as iron wool. Or water, which will burn upon exposure to fluorine.

This video, from the Periodic Videos collection, shows some reactions of fluorine with things such as iron wool, charcoal briquettes, and a lump of sulfur:

Now, fluorine may go about obtaining its extra electron very violently, prying it out of the grasp of any other atoms it comes across if it can (barring helium and neon); however, once it has achieved the low energy state it finds itself in, it's actually quite tame. Fluorine with this extra electron is called fluoride (which is an ion since it is no longer electrically neutral), and it is quite happy to share this electron with another atom leading to exceptionally strong chemical bonds.

In fact, you probably have more exposure to fluoride than you might think if you use Teflon cookware. Teflon is the brand name for a chemical known as polytetrafluoroethylene, which is pretty much nothing but long chains of carbon atoms each with two fluorine atoms attached to it. Because these fluorine atoms bind so strongly to the carbon atoms they are highly reluctant to attract anything else, which is why Teflon is so slippery (it is the third most slippery substance known, and in fact is the only known material to which a gecko cannot stick).

Fluoride is also useful in another manner than ties back to number seven on the clock: remember how in the discussion of the Mohs scale of mineral hardness I mentioned that your teeth are made of a form of apatite and thus had a hardness of about five? Well, it turns out that tooth enamel is vulnerable to decay in acidic environments, such as your mouth after drinking anything acidic (like soda) or consuming sugar (bacteria in your mouth create various acids as they consume the sugar, again lowering the pH around your teeth).

Now, it turns out that if you have fluoride ions in your mouth, they will tend to bind themselves over time to the surface of your teeth, changing the enamel from hydroxyapatite to fluorapatite, which is much more resistant to attack by acids (in essence, the fluorine atoms bind tightly to the tooth enamel, making it harder for other materials such as acids to reach the enamel). Many toothpastes now contain fluoride, and it is often added in small amounts to drinking water. The nice thing about fluoride ions is that they're inert enough that they really don't interact much with the rest of you, passing through harmlessly.

So there you go. The universe's most reactive (and one of the more dangerous) elements, serving double duty to make our dish-cleaning less tedious and our teeth better protected from cavities. All around a fascinating element, and I highly recommend you read up on it yourself – there's much more to be said about it than I can fit in this post.

Anyway, check back next time for a number from physics and biology! Click here to jump directly to it.

Science Clock Series: Part VIII

Today's number comes from astronomy, and is given by:

\[\approx\text{distance to center of Milky Way (kpc)}\]

This one is pretty straight forward, though it requires a fair amount of exposition. The Milky Way, of course, is the galaxy within which we all live. As far as we can tell from our inside perspective, it is a barred spiral galaxy, like many others throughout the universe. 

The letters "kpc" stand for "kiloparsec," an astronomical unit of distance. "Kilo" is the SI prefix for a thousand, so we're dealing with a thousand parsecs. Just what is a parsec, though? A parsec is defined as the distance at which an object has an astronomical parallax of one arcsecond. Parallax is the way objects appear to move when you look at them from two different positions, when compared to even more distant objects.

(To see this effect, close one eye and line up your thumb at arm's length with an object across the room. Now switch eyes, and notice how your thumb is no longer in line with the object. This is the reason we have two eyes, in fact; our brain takes the slight differences in the angles between them and interprets it as distance. If you can measure the parallax of an astronomical object, you can mathematically work out its distance in a similar manner.)

An arcsecond, as I've discussed here before on this blog, is a unit of angular measurement (and a very small one at that). For comparison, there are 60 arcseconds per arcminute, and the full Moon (and Sun) are about 30 arcminutes in angular diameter. Thus an arcsecond is about 1/1800 the width of the full Moon.

This is a pretty small amount. And yet, there are no stars within 1 parsec of the Sun, so every star in the sky has a parallax smaller than 1 arcsecond. This is much, much too small to be noticed with the naked eye, and it wasn't until 1838 that the first measurement of a star's parallax was made by the German astronomer Friedrich Bessel. (The closest star to the Sun, Proxima Centauri, is 1.3009 parsecs away, or 4.243 light-years.)

Anway, that's how you define a parsec, but what does it mean in units your or I might be more familiar with? When you do the math a parsec works out to be approximately 3.26 light-years, or 30.9 trillion kilometers, or 19.2 trillion miles. A kiloparsec, then, is a massive 30.9 quadrillion kilometers, or 19.2 quadrillion miles, or 3,260 light-years.

This...is a long way. It is simply too large a distance for me to truly comprehend it. And yet we need such large units to meaningfully talk about our galaxy, which is around 31-37 kiloparsecs across (100,000-120,000 light-years). It's hard to put a solid number on it since the galaxy has no hard edge, but rather fades out around the edges. This gives it a radius of about 15-18 kiloparsecs, and as far as we can tell, the Solar System is located between about 8.0 and 8.7 kiloparsecs from the center of the galaxy (roughly 26,000 to 28,000 light-years), putting it about halfway out, nestled between two of the Milky Way's spiral arms.

Check back next time for a number from chemistry! Click here to jump directly to it.